【質問解説2】二次関数の最大最小と場合分け

YouTube : https://youtu.be/EsEey_A6y0U

前回の記事で【質問解説1】二次関数と不等式の問題を解説しました。

今回は二つ目の「二次関数の最大最小と場合分け」の解説です。たぶん二次関数の問題では一番難しい部類の問題ですね。

今回の問題は「グラフ固定、範囲が動く」問題ですが、実力のない僕がこれをぱっとみていやなのは、範囲が「P〜2P+1」となっていることです。これが「P〜P+2」みたいな形だととても簡単なのですが。なので自分でも腕試しのようなつもりで解いてみました。

問題

解答

生徒の答案

ノート

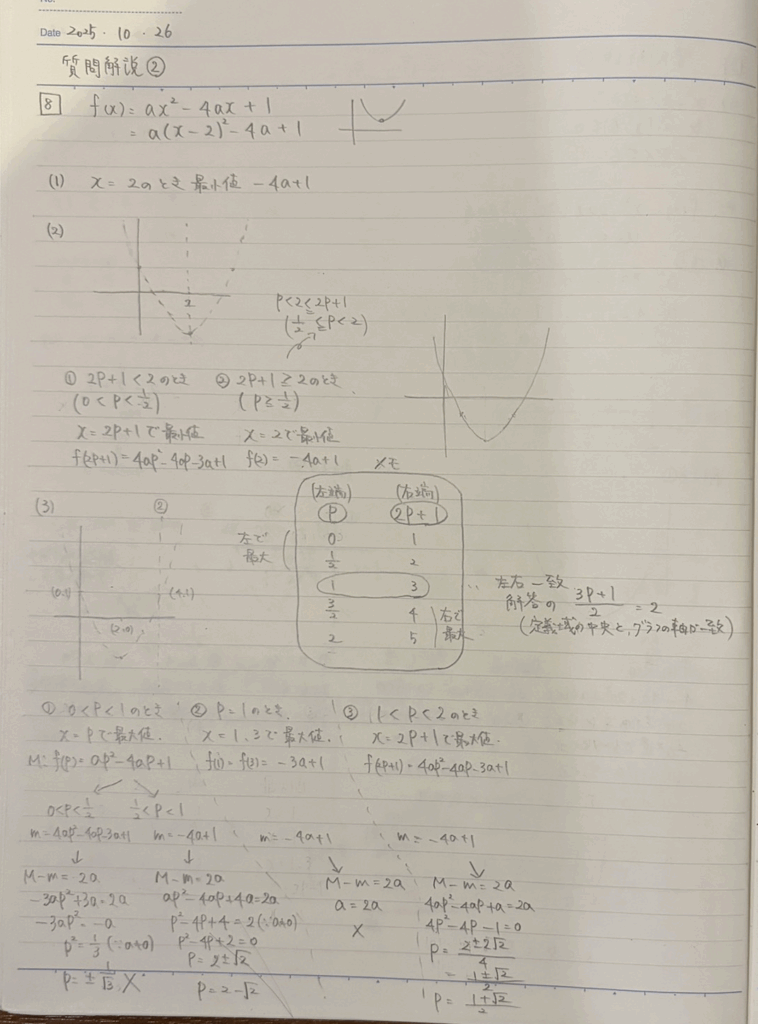
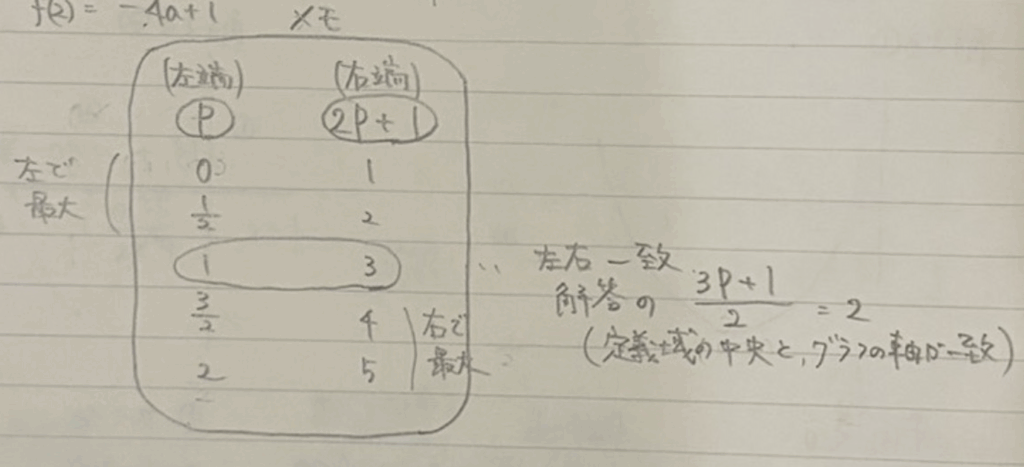
こういう問題はほんと「場合分けができるかどうか」だけがポイントだなと僕は考えています。今回は場合分けに頭を使ってしまって爆発しかけたのですが、頭の中でごちゃごちゃしていることを、メモ書きのところで数字をあてはめながら整理してみると、とたんにすっきりしました。場合分けのうち、真ん中のところをみつけると、あとは範囲を左や右にずらしながらそれぞれ計算していくだけです。

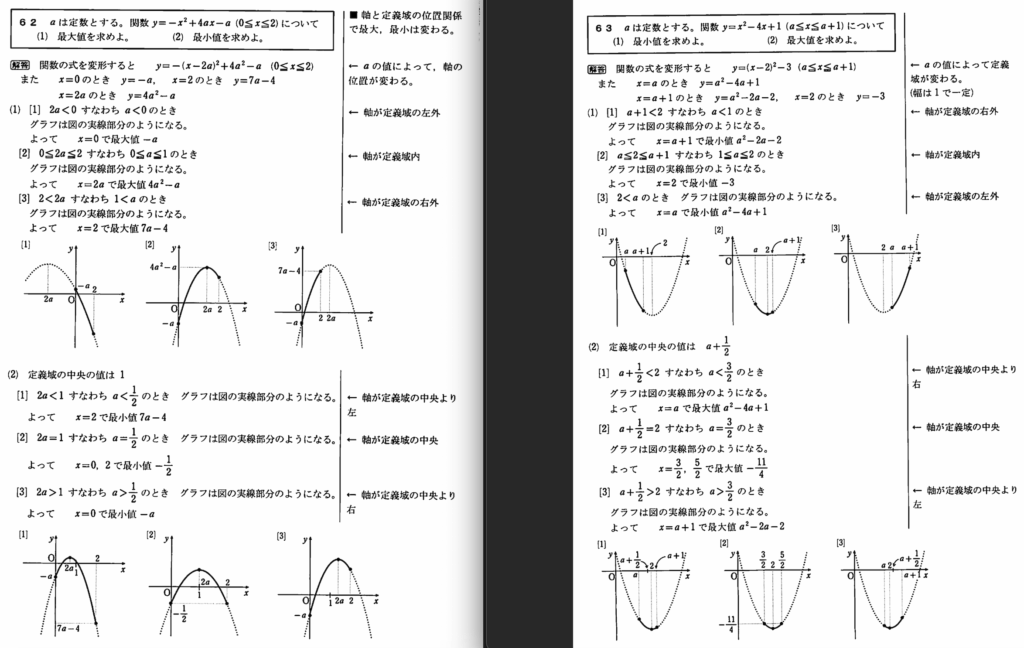
僕は明日の県模試どうこうよりも、まずは基礎をしっかりすることが大事だと思います。問題集にはおそらくこの2つの問題がならんでいると思います。「63:範囲固定でグラフが動く」「64:グラフ固定で範囲が動く」。まずはこの2つができればこの先大丈夫で、あとは問題ごとに対応していく形ですね。

YouTubeでの解説動画
【数学1A】2次関数と最大・最小 (①グラフが動く)
【数学1A】2次関数と最大・最小 (②範囲が動く)

コツは2点。
・最大値も最小値も3つに場合分けできるので、グラフをかきながらまずは真ん中を考える。
・「最大値最小値を答えよ」とまとめてきかれても、まずはべつべつに考えてあとで数直線をかきながら答えをつくっていく。

ふつうはなかなか難しい問題ですけど、この2問ができれば簡単に感じると思います。

ということで2つ目の質問解説でした。